امواج الکترومغناطیس چیست ؟

در این مقاله معادلات ماکسول و نحوه بدست آوردن آن‌ها را توضیح دادیم. در این قسمت قصد داریم تا از این معادلات، استفاده کرده و امواج الکترومغناطیسی را تعریف و توصیف کنیم. به دو میدان الکتریکی و مغناطیسی عمود به هم، که با زمان و مکان نوسان کرده و در جهتی خاص حرکت می‌کنند، موج الکترومغناطیسی گفته می‌شود. در ادامه در مورد ویژگی این دو میدان عمود به هم و ارتباط آن‌ها با یکدیگر بحث خواهد شد. همچنین پیشنهاد می‌کنیم جهت آشنایی با انواع مختلف امواج الکترومغناطیسی به مقاله «طیف الکترومغناطیسی — به زبان ساده» رجوع کنید.

امواج الکترومغناطیسی تخت

جهت بررسی ویژگی‌های امواج الکترومغناطیسی، مطابق با انیمیشن زیر موجی را در نظر بگیرید که در جهت مثبت محور x در حرکت است.

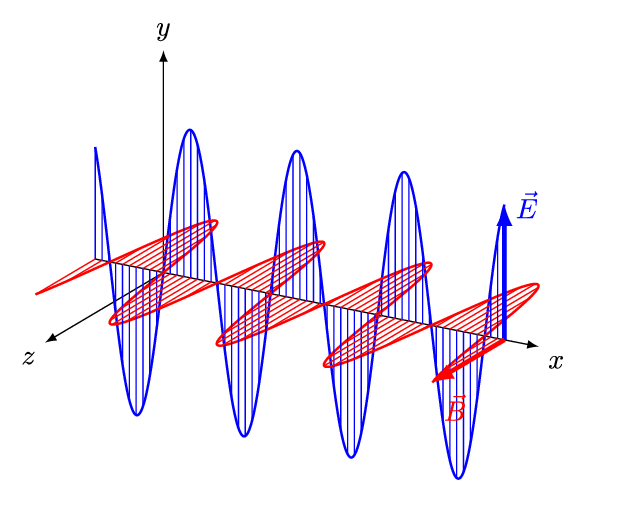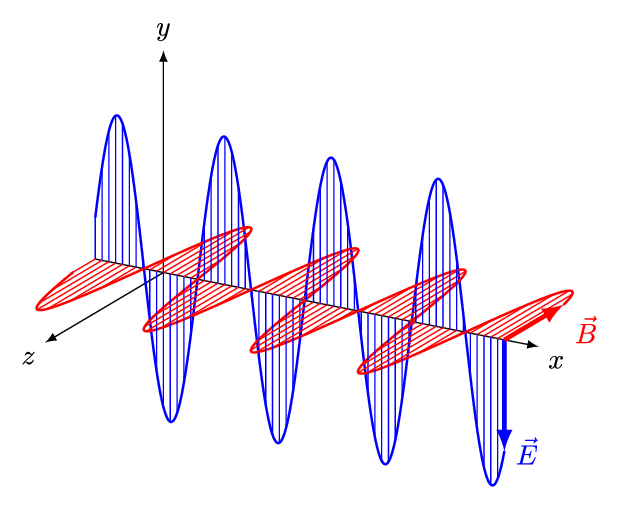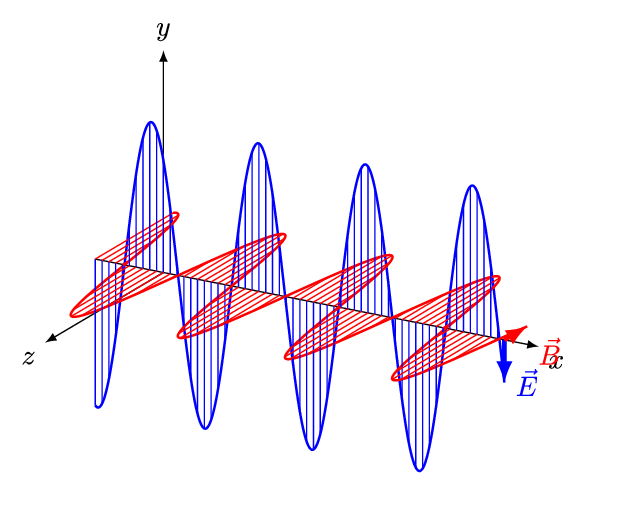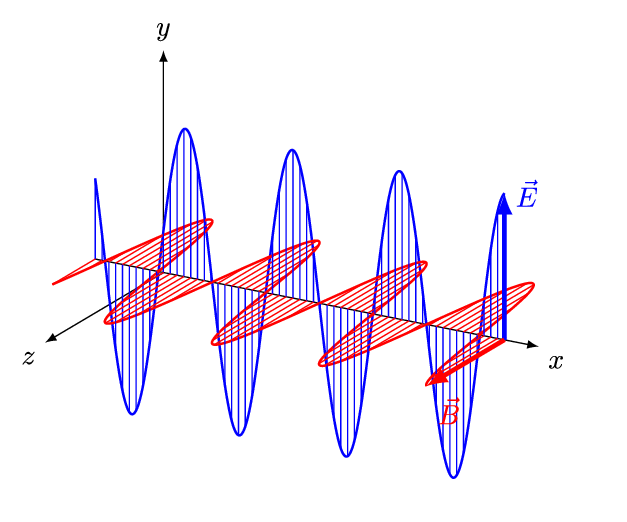
مطابق با انیمیشن بالا اندازه میدان الکتریکی (E) در راستای y و اندازه میدان مغناطیسی (B) در راستای z با زمان تغییر می‌کنند. موجی که در بالا شرح داده شد، نمونه‌ای از یک موج تخت محسوب می‌شود. هم‌چنین با توجه به این که هر دو میدان به جهت انتشار عمود هستند، به این نوع از موج، موج عرضی نیز گفته می‌شود. در امواج عرضی، جهت انتشارِ موج، در جهت بردار یکه E→×B→E×B است.

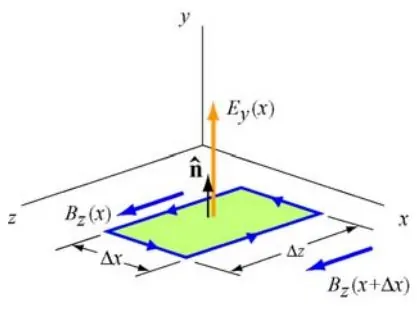
با استفاده از معادلات ماکسول، می‌توان اندازه ‌میدان‌های الکتریکی و مغناطیسی را یافت. بدین منظور مطابق با تصویر زیر منحنی مستطیلی شکلی را در صفحه x-y در نظر بگیرید.

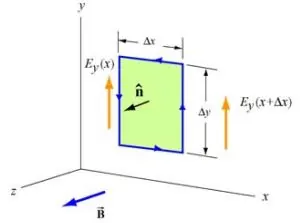
سمت چپ حلقه در موقعیت x و سمت راست در x+Δx قرار گرفته است. پایین حلقه نیز در y و بالای آن در y+Δy است. جهت ساده‌سازی، بردار عمود به حلقه را برابر با n^=k^n=k تصور کنید. با نوشتن قانون القای فارادی برای صفحه تشکیل شده از این حلقه داریم:

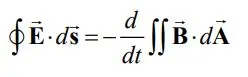
سمت چپ معادله بالا برابر است با:

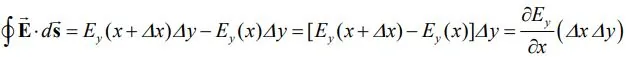
رابطه ۱

در رابطه بالا از بسط تیلور زیر استفاده شده:

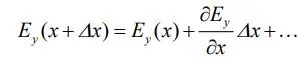
از طرفی نرخ تغییرات میدان مغناطیسی در دیفرانسیل dA برابر است با:

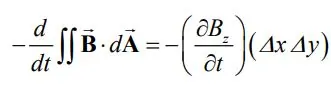
رابطه ۲

با برابر قرار دادن رابطه ۱ و ۲ و تقسیم کردن آن‌ها به Δy داریم:

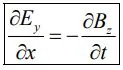
رابطه ۳

رابطه بالا تغییرات میدان الکتریکی در مکان را بر حسب تغییرات میدان مغناطیسی در زمان نشان می‌دهد. اگر بخواهیم تغییرات میدان الکتریکی را در زمان بر حسب میدان مغناطیسی بیان کنیم، حلقه‌ای را مطابق با شکل زیر در نظر می‌گیریم.

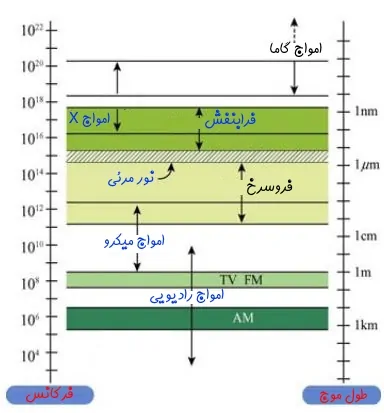
امواج الکترومغناطیسی با سرعت نور منتشر می‌شوند. هم‌چنین خود نور نیز نوعی موج الکترومغناطیسی است. طیف الکترومغناطیسی امواج مختلف در جدول زیر نشان داده شده است.

معادله موج تک‌ بعدی

می‌توان به طور مستقیم اثبات کرد که هر تابعی به صورت (ψ(x±vt در معادله موج صادق خواهد بود. این بیان در ادامه اثبات شده است. جهت اثبات، در ابتدا متغیر x’=x±vt را تعریف می‌کنیم. با استفاده از این تعریف، مشتقات زمانی و مکانی این متغیر به صورت ∂x′/∂x=1∂x′/∂x=1 و ∂x′/∂t=±v∂x′/∂t=±v خواهند بود. در نتیجه با استفاده از قانون مشتق‌گیری زنجیره‌ای داریم:

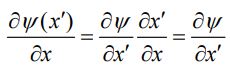
در نتیجه مشتق دوم (‘ψ(x برابر است با:

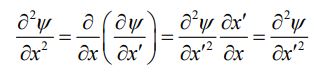
با روشی مشابه مشتق‌گیری زمانی تابع ψ(x′)ψ(x′) را می‌توان نسبت به زمان و مطابق با عبارت زیر بدست آورد.

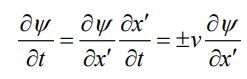
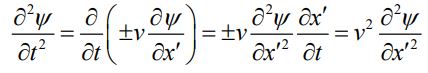
با مقایسه رابطه ۹ و ۱۰ داریم:

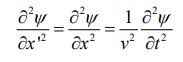
عبارت بالا نشان می‌دهد که $$\psi (x\pm vt)$$ در رابطه موج یک‌بعدی صدق می‌کند. معادله موج مثالی از معادله دیفرانسیلی خطی است؛ در نتیجه که اگر ψ1(x,t)ψ1​(x,t) و ψ2(x,t)ψ2​(x,t) پاسخ‌های معادله دیفرانسیل مذکور باشند، در این صورت ψ1(x,t)+ψ2(x,t)ψ1​(x,t)+ψ2​(x,t) نیز در معادله دیفرانسیل موج صادق خواهند بود.

بنابراین تا به این‌جا دو معادله را برای یک موج الکترومغناطیسی مطابق با رابطه زیر یافتیم و ثابت کردیم که هر کدام از آن‌ها موجی تک‌ بعدی هستند [یک معادله برای میدان الکتریکی و یک معادله برای میدان مغناطیسی].

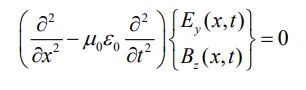
یکی از پاسخ‌های ممکن برای دو معادله بالا به صورت زیر است:

مطابق با رابطه بالا، تغییرات میدان‌ها به صورت سینوسی در نظر گرفته شده و دامنه آن‌ها نیز برابر با E₀ و B₀ فرض شده‌اند. مقدار k یا همان عدد موج را می‌توان بر حسب طول موجِ λ، بصورت زیر بیان کرد:

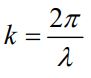
فرکانس زاویه‌ای ω نیز برابر است با:

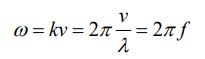
در رابطه بالا f برابر با فرکانس خطی موج است. در فضای خالی (خلاء) سرعت موج الکترومغناطیسی برابر با سرعت نور است (v=c). نمونه‌ای از یک موج الکترومغناطیسیِ سینوسی در شکل زیر نشان داده شده است.

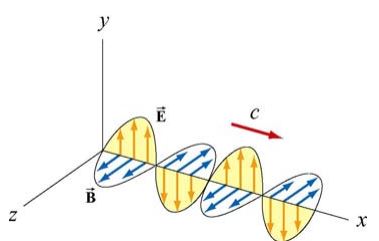
همان‌طور که در شکل بالا نیز می‌بینید، در یک موج تخت میدان‌های B→B و E→E همواره هم‌فاز هستند. در حقیقت در یک زمان و مکان، میدان‌های الکتریکی و مغناطیسی ماکزیمم شده و در یک زمان نیز می‌نیمم می‌شوند. جهت بدست آوردن مقادیر E₀ و B₀ بر حسب یکدیگر، می‌توان از معادلات معرفی شده برای میدان مغناطیسی و الکتریکی به‌شکل زیر مشتق جزئی گرفت:

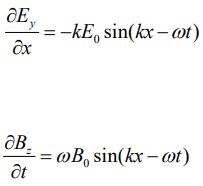
از طرفی در بالا رابطه زیر را نشان دادیم:

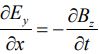
با برابر قرار دادن دو معادله معرفی شده در رابطه ۱۱، به عبارت E₀k=ωB₀ می‌رسیم؛ در نتیجه رابطه بین دامنه دو میدان به‌شکل زیر بدست می‌آید.

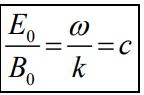
معادلات بالا ویژگی‌ موج‌های تخت عرضی را توصیف می‌کنند. ویژگی اصلی این نوع از موج‌ها به‌طور خلاصه به شرح زیر هستند:

1. این نوع موج به صورت عرضی است. دلیل عرضی بودن آن‌ها این است که میدان‌های مغناطیسی و الکتریکی در هر لحظه به یکدیگر عمود بوده و جهت انتشار آن‌ها نیز به جهت حرکت موج عمود است. در حقیقت جهت انتشار موج در جهت بردار یکه E^×B^E×B است.
2. حاصلضرب داخلی دو بردار E→E و B→B در هر لحظه برابر با صفر است.
3. نسبت اندازه دامنه میدان‌ها برابر است با:
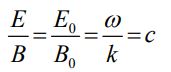
4. سرعت انتشار این موج در خلاء برابر با سرعت نور یا همان 1μ0ϵ0μ0​ϵ0​​1​ است.
5. امواج الکترومغناطیسی از قانون جمع آثار پیروی می‌کنند.

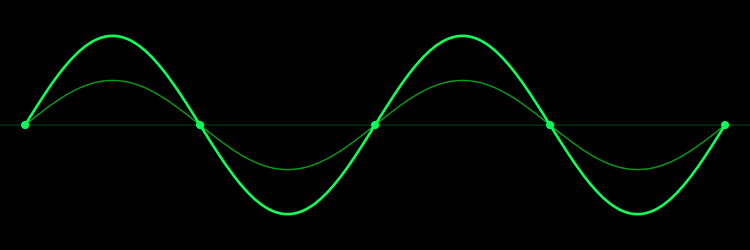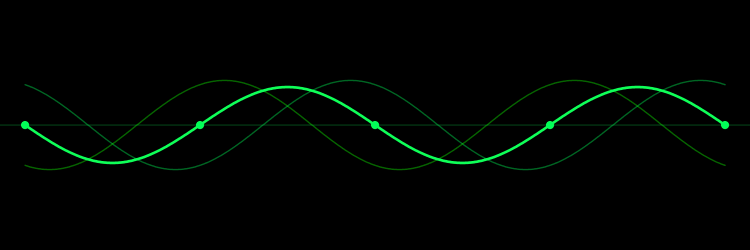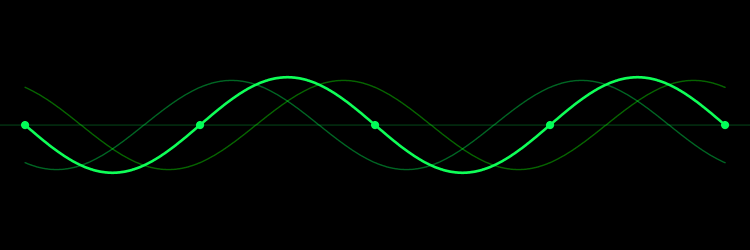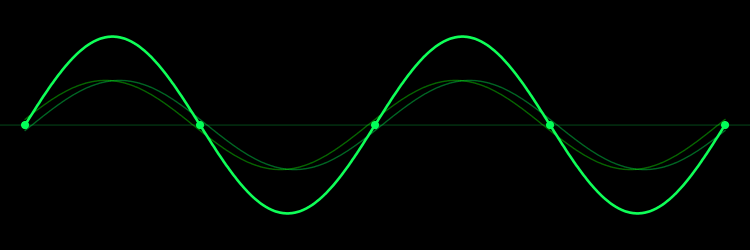
به نقاط بیان شده در بالا، نقاط گرهی گفته می‌شود. هم‌چنین به صفحاتی که در آن، گره‌ها قرار دارند، «صفحات گره» (Nodal planes) گفته می‌شود. در انیمیشنی که در زیر ارائه شده می‌توانید دو موج رفت و برگشتی که با یکدیگر جمع شده‌اند و موج ساکنِ اصلی را مشاهده کنید.